Graficacionblog2012
domingo, 20 de mayo de 2012
viernes, 18 de mayo de 2012
miércoles, 16 de mayo de 2012
INVESTIGACION DE USO DE LA GRAFICACION
Medicina.
La Informática
Gráfica está jugando un papel cada vez más importante en campos como la
diagnosis médica y cirugía. A través de imágenes el médico diagnostica
enfermedades y el cirujano es capaz de realizar intervenciones quirúrgicas con menores
riesgos.
Tecnología:
Maquinas.
Robótica.
Telemedicina.
Rayos X.
Educación.
Donde se están
introduciendo los métodos multimedia e hipertexto para mejorar las actitudes
hacia el aprendizaje de los alumnos de edades tempranas.
Es muy común utilizar métodos de gráficas por computadora para producir películas, videos musicales y programas de televisión. En ocasiones, se despliegan sólo imágenes gráficas y otras veces, se combinan los objetos con los actores y escenas en vivo. Por ejemplo, en una escena gráfica creada para la película Start Treck - The Wrath of Khan, se dibujan en forma de armazón el planeta y la nave espacial y se sonbrean con métodos de presentación para producir superficies sólidas.
Es muy común utilizar métodos de gráficas por computadora para producir películas, videos musicales y programas de televisión. En ocasiones, se despliegan sólo imágenes gráficas y otras veces, se combinan los objetos con los actores y escenas en vivo. Por ejemplo, en una escena gráfica creada para la película Start Treck - The Wrath of Khan, se dibujan en forma de armazón el planeta y la nave espacial y se sonbrean con métodos de presentación para producir superficies sólidas.
Tecnología:
Pizarrones
táctiles.
Computadoras.
Publicidad
Los métodos de
Informática Gráfica se utilizan de forma generalizada tanto en aplicaciones de
bellas artes como en aplicaciones de arte comercial y publicidad. La mayoría de
ilustraciones que encontramos en las revistas, carátulas de discos etc, se
realizan con paquetes informáticos de Diseño Gráfico.
Tecnología:
Cámaras.
Imprenta.
Software:
Paint.
Photoshop.
Entretenimiento.
En la actualidad
se utilizan comúnmente los métodos de Informática Gráfica en la producción de
cine, videojuegos etc.
Es muy común utilizar métodos de gráficas por computadora para producir películas,
videos musicales y programas de televisión. En ocasiones, se despliegan sólo
imágenes gráficas y otras veces, se combinan los objetos con los actores y
escenas en vivo. Por ejemplo, en una escena gráfica creada para la película
Start Treck - The Wrath of Khan, se dibujan en forma de armazón el planeta y la
nave espacial y se sonbrean con métodos de presentación para producir
superficies sólidas. Al igual que pueden aparecer personas en forma de armazón
combinadas con actores y una escena en vivo.
Tecnología:
Computadoras.
Software:
3D max
Maya
Blender
Flash
martes, 24 de abril de 2012
INVESTIGACION UNIDAD #4
La función glColor
define el color de rellenado actual y lleva como parámetros los valores de las
componentes RGB del color deseado y, opcionalmente, un cuarto parámetro con el
valor alpha. Estos parámetros son flotantes y se mueven en el rango [0.0,1.0].
Con ello se pueden componer todos los colores del modo
de video usado en ese instante.
Clásicas:
Iluminación local
Son aquellos en
los que se considera que la intensidad de luz en un punto de la superficie de
un objeto se debe exclusivamente a las Fuentes luminosas.
Cálculos de
iluminación por vértices
Para aplicar
iluminaciona un objeto necesitamos asociar un vector normal a cada vertice del
objeto. Cuando tenemos la normal calculada tenemos que normalizarla, o
sea, dividir ese vector por su propio modulo para que sea unitario, pero
también podemos hacer que se encargue la OpengGl activando la normalización con
el comando glEnable GL_NORMALIZE o desactivarla con glDisable GL_NORMALIZE.
El usar
GL_NORMALIZE dependerá de nuestra aplicación ya que si forzamos a que sea
OpenGl el que las utilice se ralentiza por que le estamos obligando a hacer mas
cálculos de los que debe.
Para definir las
normales en opengl utilizaremos la función glNormal3f(X,Y,Z) por ejemplo para
definir una cara con 4 vértices la definiremos de la siguiente manera:
GlBegin
GL_QUADS
glNormal3f
nX,nY,nZ
glvertex3f x,y,z
glvertex3f x,y,z
glvertex3f x,y,z
glvertex3f x,y,z
glEnd
Es decir, cada
vez que queremos asociar una normal a un vértice usamos glNormal y el vértice/s
que siguen se asocia a esta normal.
Posterior relleno
de triángulos
Rastering. Para
ello se realizan varias fases de procesamiento por Pixel.
-Comprobar si
cada nuevo pixel es visible o no (comprobación de profundidad).
-Interpolación
lineal del color para el nuevo pixel (método de Gouraud).
-Si existe una
textura definida o transparencia, efectuar la modificación de color
correspondiente.
Se trata de la
última fase, en ocasiones la más costosa del proceso, por lo que es la primera
que se suele integrar en el hardware gráfico. En esta etapa se trata de asignar
colores a los pixeles correspondientes al interior de cada triángulo proyectado
que cae dentro del área de visualización. Los colores asignados deben
calcularse por el método de Gouraud, interpolando linealmente entre los colores
de los tres vértices.
Renderizado en
tiempo real
La idea
fundamental del procesado en tiempo real es que todos los objetos deben ser
descompuestos en polígonos. Estos polígonos serán descompuestos a su vez en
triángulos. Cada triangulo será proyectado sobre la ventana bidimensional y
rellenado con los colores adecuados para reflejar los efectos de la
iluminación, texturas, etc. Una vez se han generado los triángulos, en la
pipeline existen dos partes claramente diferenciadas: una primera etapa de
operaciones realizadas sobre cada uno de los vértices, y después de que estos
se proyecten sobre la ventana, entonces comienza una segunda fase de cálculos
realizados para cada pixel cubierto por los triángulos.
Realistas:
iluminación global
Son
aquellos en los que se considera que la intensidad de luz en un punto de la
superficie de un objeto se debe a las fuentes luminosas y al resto de los
elementos existentes en la escena.
Trazado de rayos
El trazado de
rayos computa la interacción de la luz desde un punto de vista determinado y es
particularmente adecuado para superficies reflectantes. Puede utilizarse como
propiedad especifica de un determinado material. Se traza un rayo desde la
posición del observador a través de cada uno de los píxeles del plano de
proyección (una de las ventajas del raytracing es que los rayos que se procesan
son sólo los rayos que parten del observador ), y por cada uno de estos rayos
trazados se busca si interseca con alguno de los objetos que se representan; si
no se encuentra ninguna intersección, para ese pixel, no se sigue el proceso y
se le hace corresponder, por defecto, un color de fondo.
Radiosidad
En el estado
inicial la escena consta de dos tipos de objetos: objetos que emiten luz y
objetos que reciben luz. A partir de aquí, en una primera vuelta, se computa la
luz que recibe cada objeto en una aproximación más exacta, cada parte de un
objeto, según una subdivisión cuya densidad puede precisarse en sucesivas
aproximaciones. Cada una de estas partes, según su grado de reflexividad, su
orientación y su distancia con respecto a las fuentes de luz original, se
convertirá en una segunda vuelta, en un nuevo emisor de energía lumínica, una
fuente de luz secundaria que iluminara a su vez a los objetos que le rodean.
Cálculos de iluminación
por pixel
La iluminación
por píxel en tiempo real es una tecnología revolucionaria ofrecida como
primicia por NVIDIA Shading Rasterizer. La iluminación dinámica a nivel de
píxel libera a los desarrolladores de las restricciones de otros sistemas de
iluminación y pone a su alcance toda una gama de sofisticados efectos. Antes de
que el color final del píxel sea decidido, un cálculo de iluminación debe ser
computado para sombrear a los píxeles basados en alguna luz que puede estar
presente en la escena.
Alto Acabado
Sombreado
Constante o plano. Un cálculo para todo el polígono. Obtenemos una
intensidad que aplicamos a un conjunto de puntos de un objeto (p.ej. todo
un triángulo). Aceleramos el proceso de síntesis. Correcto si se
verifica: Fuente de luz en el infinito. Observador en el infinito. El polígono
representa una superficie plana real del objeto que se modela y no es una
aproximación de un objeto curvo.
Sombreado Constante ó Plano
Un cálculo para
todo el polígono
Los tres
vectores, l, n y v, pueden variar según se va entre puntos sobre una
superficie.
• Para un
polígono plano, n es constante.
• Si se asume un
observador distante, v es constante sobre el polígono.
• Si la fuente de
luz es distante, l es constante.
Si los tres vectores
son constantes, entonces el cálculo de sombreado se lleva a cabo una sola vez
para cada polígono, y se asignará la misma sombra a cada punto en el polígono.
Sombreado plano mostrará
diferencias de sombreado entre los polígonos.
Modelo de Reflexión Phong
El modelo de reflexión de Phong es eficiente y suficientemente
aproximado a la realidad física para producir buenas imágenes, bajo una
variedad de condiciones de luz y propiedades de materiales. Apoya los tres
tipos de interacciones material-luz: ambiente, difusa y especular. Si se tiene
un conjunto de fuentes puntos, con componentes independientes para cada uno de
los tres colores primarios para cada uno de los tres tipos de interacciones
material-luz.
Ray Tracing
En muchas formas, ray tracing es una extensión al enfoque de rendering
con un modelo de iluminación local. Está basado en la observación previa que,
de los rayos de luz saliendo de una fuente, los únicos que contribuyen a la
imagen son aquellos que entran al lente de la cámara sintética y pasan por el
centro de proyección.
Buffer de Profundidad.
El Z-Buffer se
basa en que al generar la posición de un punto en la pantalla la computadora
reserve una zona de memoria especial, llamada Z-Buffer, información relacionada
con la profundidad del punto que ocupa en la escena representada. Cuando el
ordenador representa un nuevo punto consulta el Z-Buffer del píxel que
corresponde en pantalla. Si el valor que ya existe en el píxel es mayor que el
que posee el nuevo punto, el sistema asume que este último es el visible y lo
sustituye en la memoria del Z- Buffer.
Buffer Stencil.
Stencill Buffer es
una memoria intermedia que analiza y actualiza píxeles (con sus operaciones) junto
con “depth buffer” o buffer de profundidad. Añade planos de bits adicionales
para cada píxel además de los bits de color y profundidad.
Stencil buffer es
similar al buffer de profundidad en que los dos son colección de planos de bit
que no se pueden mostrar. Del mismo modo que el buffer de profundidad asocia a
cada píxel de la ventana un valor de profundidad, el stencil buffer asocia su
propio valor a cada píxel mostrado. Cuando el buffer de profundidad esta
activado los valores de profundidad son usados para aceptar o rechazar
fragmentos, del mismo modo los valores de Stencil buffer son usados para
aceptar o rechazar fragmentos.
Buffer de Acumulacion
Normalmente se usa
un buffer de acumulación para unir las 2 imágenes
Fuentes de Luz
La luz puede dejar una superficie mediante dos procesos fundamentales:
- Emisión propia
- Reflexión
Normalmente se
piensa en una fuente de luz como un objeto que emite luz solo mediante fuentes
de energía internas, sin embargo, una fuente de luz, como un foco, puede
reflejar alguna luz incidente a esta del ambiente. Este aspecto no será tomado
en cuenta en los modelos más sencillos.
Fuentes de Luz Distantes
La mayoría de los cálculos de sombreado requieren la dirección de un
punto sobre la superficie a la fuente de luz. Según se mueve a lo largo de la
superficie, se debe recomputar este vector para calcular la intensidad en cada
punto, una computación que es una parte significativa del cálculo del
sombreado. Sin embargo, si la fuente de luz está lejos de la superficie, el
vector no cambiará mucho según se mueve de un punto a otro, al igual que la luz
del sol da en todos los objetos cercanos entre si con el mismo ángulo.
Fuentes de Color
No solamente las fuentes de luz emiten diferentes cantidades de luz en
diferentes frecuencias, pero también sus propiedades direccionales varían con
la frecuencia. Por lo tanto, un modelos físicamente correcto puede ser muy
complejo. Para la mayoría de las aplicaciones, se puede modelar fuentes de luz
en base a tres componentes primarios, RGB, y puede usar cada uno de los tres
colores fuentes para obtener el componente de color correspondiente que un
observador humano vería.
Luz Ambiente
La luz ambiente ilumina por igual todas las zonas en sombra para simular
el efecto de interacción entre objetos que hace que las partes en sombra de los
objetos queden parcialmente iluminadas. En algunos cuartos, las luces se
diseñan y ubican para proveer iluminación uniforme en el cuarto. Tal
iluminación se logra mediante fuentes grandes con difusores cuyo propósito es
esparcir la luz en todas las direcciones. Se puede crear una simulación precisa
de tal iluminación, modelando todas las fuentes distribuidas, y luego
integrando la iluminación de estas fuentes en cada punto de una superficie
reflectora. Hacer tal modelo y generar la escena sería una tarea formidable
para un sistema gráfico, especialmente si se desea ejecución en tiempo real.
Spotlights (direccionales)
Los spotlights se caracterizan por un rango delgado de ángulos por
los cuales se emite luz. Se puede construir un spotlight sencillo de una fuente
de punto limitando los ángulos de donde la luz de la fuente se puede ver. Se
puede usar un cono cuyo ápice está en ps, apuntando en la dirección ls, y cuyo
ancho está determinado por el ángulo θ.
BIBLOGRAFIA
http://informatica.uv.es/iiguia/AIG/web_teoria/tema3.pdf
http://www.azrodin.com/2009/09/generacion-de-sombras-con-stencil-buffer/
http://cannes.itam.mx/Alfredo/Espaniol/Cursos/Grafica/Sombreado.pdf
http://sabia.tic.udc.es/gc/Contenidos%20adicionales/trabajos/3D/modelosIlumionacion/introduccion_intensidad_completa.html
jueves, 19 de abril de 2012
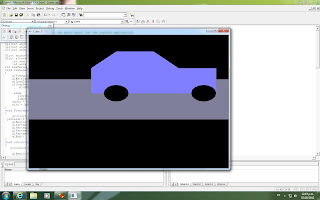
CARRO 2D EN MOVIEMIENTO
//#include "stdafx.h"
// moverpelota.cpp : Defines the entry point for the console application.
//
//#include "stdafx.h"
#include <GL/glut.h>
GLfloat anguloCuboX = 0.0f;
GLfloat anguloCuboY = 0.0f;
GLfloat anguloEsfera = 0.0f;
GLint ancho=900;
GLint alto=600;
int ang =0 ;
int movx = 0;
int hazPerspectiva = 0;
void reshape(int width, int height)
{
glViewport(0, 0, width, height);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(hazPerspectiva)
gluPerspective(60.0f,(GLfloat)width/(GLfloat)height, 1.0f, 20.0f);
else
glOrtho(-4,4, -4, 4, 1, 10);
glMatrixMode(GL_MODELVIEW);
ancho = width;
alto = height;
}
void Piso(void)
{
glColor3f(0.5f, 0.5f, 0.6f);
glScalef(1.5f,0.0f,1.5f);
glBegin(GL_QUADS); //cara abajo
glVertex3f( 10.0f,-10.0f, -10.0f);
glVertex3f( 10.0f,-10.0f, 10.0f);
glVertex3f(-10.0f,-10.0f, 10.0f);
glVertex3f(-10.0f,-10.0f, -10.0f);
glEnd();
}
void carro(void)
{
glColor3f(0.5f, 0.5f, 1.0f);
glBegin(GL_POLYGON); //carro
glVertex3f(-1.5f,0.5f, -2.0f);
glVertex3f( 3.5f,0.5f, -2.0f);
glVertex3f(3.5f,2.0f, -2.0f);
glVertex3f(2.0f,2.0f, -2.0f);
glVertex3f(1.f,3.0f, -2.0f);
glVertex3f(-0.5f,3.0f, -2.0f);
glVertex3f(-1.5f,2.0f, -2.0f);
glEnd();
}
void display()
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glTranslatef(0.0f, 0.0f, -5.0f);
glRotatef(15, 1.0f, 0.0f, 0.0f);
glRotatef(15, 0.0f, 1.0f, 0.0f);
Piso();
// dibuja rueda
//dibuja 2da rueda
glLoadIdentity();
glColor3f(-1.0f, 0.0f, 1.0f);
glTranslatef(movx,0.0,0.0);
carro();
glLoadIdentity();
glTranslatef(-.5f,0.5f,-1.0f);
glColor3f(0.0f, 0.0f, 0.0f);
glRotatef(ang,1.0,0.0,0.0);
glTranslatef(movx,0.0,0.0);
glutSolidSphere(0.5f, 16, 16);
glLoadIdentity();
glTranslatef(3.0f,0.5f,-1.0f);
glColor3f(0.0f, 0.0f, 0.0f);
glRotatef(ang,1.0,0.0,0.0);
glTranslatef(movx,0.0,0.0);
glutSolidSphere(0.5f, 16, 16);
glLoadIdentity();
glFlush();
glutSwapBuffers();
}
void init()
{
glClearColor(0,0,0,0);
glEnable(GL_DEPTH_TEST);
ancho = 600;
alto = 900;
}
void idle()
{
display();
}
void specialkeyevent( int key, int Xx, int Yy )
{
switch ( key ) {
case GLUT_KEY_LEFT:
movx-=1;
ang-=1;
display();
break;
case GLUT_KEY_RIGHT:
movx+=1;
ang-=1;
display();
break;
}
glutPostRedisplay();
}
int main(int argc, char **argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowPosition(100, 100);
glutInitWindowSize(ancho, alto);
glutCreateWindow("Cubo 1");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutIdleFunc(idle);
glutSpecialFunc(specialkeyevent );
glutMainLoop();
return 0;
}
// moverpelota.cpp : Defines the entry point for the console application.
//
//#include "stdafx.h"
#include <GL/glut.h>
GLfloat anguloCuboX = 0.0f;
GLfloat anguloCuboY = 0.0f;
GLfloat anguloEsfera = 0.0f;
GLint ancho=900;
GLint alto=600;
int ang =0 ;
int movx = 0;
int hazPerspectiva = 0;
void reshape(int width, int height)
{
glViewport(0, 0, width, height);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(hazPerspectiva)
gluPerspective(60.0f,(GLfloat)width/(GLfloat)height, 1.0f, 20.0f);
else
glOrtho(-4,4, -4, 4, 1, 10);
glMatrixMode(GL_MODELVIEW);
ancho = width;
alto = height;
}
void Piso(void)
{
glColor3f(0.5f, 0.5f, 0.6f);
glScalef(1.5f,0.0f,1.5f);
glBegin(GL_QUADS); //cara abajo
glVertex3f( 10.0f,-10.0f, -10.0f);
glVertex3f( 10.0f,-10.0f, 10.0f);
glVertex3f(-10.0f,-10.0f, 10.0f);
glVertex3f(-10.0f,-10.0f, -10.0f);
glEnd();
}
void carro(void)
{
glColor3f(0.5f, 0.5f, 1.0f);
glBegin(GL_POLYGON); //carro
glVertex3f(-1.5f,0.5f, -2.0f);
glVertex3f( 3.5f,0.5f, -2.0f);
glVertex3f(3.5f,2.0f, -2.0f);
glVertex3f(2.0f,2.0f, -2.0f);
glVertex3f(1.f,3.0f, -2.0f);
glVertex3f(-0.5f,3.0f, -2.0f);
glVertex3f(-1.5f,2.0f, -2.0f);
glEnd();
}
void display()
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glTranslatef(0.0f, 0.0f, -5.0f);
glRotatef(15, 1.0f, 0.0f, 0.0f);
glRotatef(15, 0.0f, 1.0f, 0.0f);
Piso();
// dibuja rueda
//dibuja 2da rueda
glLoadIdentity();
glColor3f(-1.0f, 0.0f, 1.0f);
glTranslatef(movx,0.0,0.0);
carro();
glLoadIdentity();
glTranslatef(-.5f,0.5f,-1.0f);
glColor3f(0.0f, 0.0f, 0.0f);
glRotatef(ang,1.0,0.0,0.0);
glTranslatef(movx,0.0,0.0);
glutSolidSphere(0.5f, 16, 16);
glLoadIdentity();
glTranslatef(3.0f,0.5f,-1.0f);
glColor3f(0.0f, 0.0f, 0.0f);
glRotatef(ang,1.0,0.0,0.0);
glTranslatef(movx,0.0,0.0);
glutSolidSphere(0.5f, 16, 16);
glLoadIdentity();
glFlush();
glutSwapBuffers();
}
void init()
{
glClearColor(0,0,0,0);
glEnable(GL_DEPTH_TEST);
ancho = 600;
alto = 900;
}
void idle()
{
display();
}
void specialkeyevent( int key, int Xx, int Yy )
{
switch ( key ) {
case GLUT_KEY_LEFT:
movx-=1;
ang-=1;
display();
break;
case GLUT_KEY_RIGHT:
movx+=1;
ang-=1;
display();
break;
}
glutPostRedisplay();
}
int main(int argc, char **argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowPosition(100, 100);
glutInitWindowSize(ancho, alto);
glutCreateWindow("Cubo 1");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutIdleFunc(idle);
glutSpecialFunc(specialkeyevent );
glutMainLoop();
return 0;
}
lunes, 16 de abril de 2012
GRAFICAS DE ESFERA Y ELIPSE
Esfera
En coordenadas cartesianas, una superficie esférica de radio r centrada en el origen de coordenadas se define como el conjunto de puntos (x,y, z) que satisface la ecuación: También podemos describir la superficie esférica de forma paramétrica, utilizando los ángulos de la latilud
y la longitud:
En coordenadas cartesianas, una superficie esférica de radio r centrada en el origen de coordenadas se define como el conjunto de puntos (x,y, z) que satisface la ecuación: También podemos describir la superficie esférica de forma paramétrica, utilizando los ángulos de la latilud
y la longitud:
X = r eos <¡> eos 0y -7t/2 < (¡> < Ttll
y = r e o s 0 sin ft -n<Q<n
z = r sin <p
Elipsoide
Una representación paramélrica de un elipsoide en función del ángulo de la latitud 0 y del ángulo de la
longitud 0:
x = rx eos 0 eos ft -7i/2 <<p<7V/2y = r e o s 0 sin ft -n<Q<n
z = r sin <p
Elipsoide
Una representación paramélrica de un elipsoide en función del ángulo de la latitud 0 y del ángulo de la
longitud 0:
y = t\ eos 0 sin ft - k < 6 < k
Z = r. Sin 0
Superelipsoide
Una representación cartesiana de un superelipsoide se obtiene a partir de la ecuación de un elipsoide incorporando dos parámetros exponenciales.
x = rAeos'1 0cos, J 0, -nI2<<t><7tt2
y = ñ eos1 ' &úx\h 0, - K < 0 < K
t~% sin*' <¡>
GLULOOKAT
Es una función de opengl que puede alterar la matriz GL_MODELBVIEW encargada de guardar el estado de todo el sistema en cuanto a transformaciones.
Parámetros:
luLookAt(eyeX, eyeY, eyeZ, atX, atY, atZ, upX, upY, upZ)
Sirve para las trasformaciones de vista con los parámetros vistos anteriormente.PROGRAMA
#include <GL/glut.h> // Once you include glut.h (you don't need gl.h or glu.h)
GLfloat X = 0.0f; // Translate screen to x direction (left or right)
GLfloat Y = 0.0f; // Translate screen to y direction (up or down)
GLfloat Z = 0.0f; // Translate screen to z direction (zoom in or out)
GLfloat rotX = 0.0f; // Rotate screen on x axis
GLfloat rotY = 0.0f; // Rotate screen on y axis
GLfloat rotZ = 0.0f; // Rotate screen on z axis
GLfloat rotLx = 0.0f; // Translate screen by using the glulookAt function (left or right)
GLfloat rotLy = 0.0f; // Translate screen by using the glulookAt function (up or down)
GLfloat rotLz = 0.0f; // Translate screen by using the glulookAt function (zoom in or out)
void glDisplayLines(void); // Did declare the function
// so I did not have to check for order of the functions
// Initialize the OpenGL window
void init(void)
{
glClearColor (0.0, 0.0, 0.0, 0.0); // Clear the color
glShadeModel (GL_FLAT); // Set the shading model to GL_FLAT
glEnable (GL_LINE_SMOOTH);
glHint(GL_LINE_SMOOTH_HINT, GL_NICEST); // Set Line Antialiasing
}
// Draw the lines (x,y,z)
void display(void)
{
glClear (GL_COLOR_BUFFER_BIT); // Clear the Color Buffer
glPushMatrix(); // It is important to push the Matrix before calling
// glRotatef and glTranslatef
glRotatef(rotX,1.0,0.0,0.0); // Rotate on x
glRotatef(rotY,0.0,1.0,0.0); // Rotate on y
glRotatef(rotZ,0.0,0.0,1.0); // Rotate on z
glTranslatef(X, Y, Z); // Translates the screen left or right,
// up or down or zoom in zoom out
// Draw the positive side of the lines x,y,z
glBegin(GL_LINES);
glColor3f (0.0, 1.0, 0.0); // Green for x axis
glVertex3f(0,0,0);
glVertex3f(10,0,0);
glColor3f(1.0,0.0,0.0); // Red for y axis
glVertex3f(0,0,0);
glVertex3f(0,10,0);
glColor3f(0.0,0.0,1.0); // Blue for z axis
glVertex3f(0,0,0);
glVertex3f(0,0,10);
glEnd();
// Dotted lines for the negative sides of x,y,z
glEnable(GL_LINE_STIPPLE); // Enable line stipple to use a
// dotted pattern for the lines
glLineStipple(1, 0x0101); // Dotted stipple pattern for the lines
glBegin(GL_LINES);
glColor3f (0.0, 1.0, 0.0); // Green for x axis
glVertex3f(-10,0,0);
glVertex3f(0,0,0);
glColor3f(1.0,0.0,0.0); // Red for y axis
glVertex3f(0,0,0);
glVertex3f(0,-10,0);
glColor3f(0.0,0.0,1.0); // Blue for z axis
glVertex3f(0,0,0);
glVertex3f(0,0,-10);
glEnd();
glDisable(GL_LINE_STIPPLE); // Disable the line stipple
glPopMatrix(); // Don't forget to pop the Matrix
glutSwapBuffers();
}
// This function is called whenever the window size is changed
void reshape (int w, int h)
{
glViewport (0, 0, (GLsizei) w, (GLsizei) h); // Set the viewport
glMatrixMode (GL_PROJECTION); // Set the Matrix mode
glLoadIdentity ();
gluPerspective(75, (GLfloat) w /(GLfloat) h , 0.10, 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt (rotLx, rotLy, 15.0 + rotLz, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
}
// This function is used for the navigation keys
void keyboard (unsigned char key, int x, int y)
{
switch (key) { // x,X,y,Y,z,Z uses the glRotatef() function
case 'x': // Rotates screen on x axis
rotX -= 0.5f;
break;
case 'X': // Opposite way
rotX += 0.5f;
break;
case 'y': // Rotates screen on y axis
rotY -= 0.5f;
break;
case 'Y': // Opposite way
rotY += 0.5f;
break;
case 'z': // Rotates screen on z axis
rotZ -= 0.5f;
break;
case 'Z': // Opposite way
rotZ += 0.5f;
break;
// j,J,k,K,l,L uses the gluLookAt function for navigation
case 'j':
rotLx -= 0.2f;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt (rotLx, rotLy, 15.0 + rotLz, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
break;
case 'J':
rotLx += 0.2f;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt (rotLx, rotLy, 15.0 + rotLz, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
break;
case 'k':
rotLy -= 0.2f;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt (rotLx, rotLy, 15.0 + rotLz, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
break;
case 'K':
rotLy += 0.2f;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt (rotLx, rotLy, 15.0 + rotLz, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
break;
case 'l': // It has a special case when the rotLZ becomes
// less than -15 the screen is viewed from the opposite side
// therefore this if statement below does not allow rotLz be less than -15
if(rotLz + 14 >= 0)
rotLz -= 0.2f;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt (rotLx, rotLy, 15.0 + rotLz, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
break;
case 'L':
rotLz += 0.2f;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt (rotLx, rotLy, 15.0 + rotLz, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
break;
case 'b': // Rotates on x axis by -90 degree
rotX -= 90.0f;
break;
case 'B': // Rotates on y axis by 90 degree
rotX += 90.0f;
break;
case 'n': // Rotates on y axis by -90 degree
rotY -= 90.0f;
break;
case 'N': // Rotates on y axis by 90 degree
rotY += 90.0f;
break;
case 'm': // Rotates on z axis by -90 degree
rotZ -= 90.0f;
break;
case 'M': // Rotates on z axis by 90 degree
rotZ += 90.0f;
break;
case 'o': // Default, resets the translations vies from starting view
case 'O':
X = Y = 0.0f;
Z = 0.0f;
rotX = 0.0f;
rotY = 0.0f;
rotZ = 0.0f;
rotLx = 0.0f;
rotLy = 0.0f;
rotLz = 0.0f;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(rotLx, rotLy, 15.0f + rotLz, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f);
break;
}
glutPostRedisplay(); // Redraw the scene
}
// called on special key pressed
void specialKey(int key, int x, int y) {
// The keys below are using the gluLookAt() function for navigation
// Check which key is pressed
switch(key) {
case GLUT_KEY_LEFT : // Rotate on x axis
X -= 0.1f;
break;
case GLUT_KEY_RIGHT : // Rotate on x axis (opposite)
X += 0.1f;
break;
case GLUT_KEY_UP : // Rotate on y axis
Y += 0.1f;
break;
case GLUT_KEY_DOWN : // Rotate on y axis (opposite)
Y -= 0.1f;
break;
case GLUT_KEY_PAGE_UP: // Rotate on z axis
Z -= 0.1f;
break;
case GLUT_KEY_PAGE_DOWN:// Rotate on z axis (opposite)
Z += 0.1f;
break;
}
glutPostRedisplay(); // Redraw the scene
}
// Main entry point of the program
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB); // Setup display mode to
// double buffer and RGB color
glutInitWindowSize (600,600); // Set the screen size
glutCreateWindow("OpenGL 3D Navigation Program");
init ();
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutKeyboardFunc(keyboard); // set window's key callback
glutSpecialFunc(specialKey); // set window's to specialKey callback
glutMainLoop();
return 0;
}
Suscribirse a:
Comentarios (Atom)